Sur les chemins de la boîte d'accord

Comment ça marche ?

Sur les chemins de la boîte d'accord

Dominique Duplouy F8CMR

La liaison de l’antenne à l’émetteur-récepteur un sujet de réflexion ? Cet article parle des transformations d’impédance effectuées par la boîte d’accord.

La boîte d’accord unit l’antenne à l’émetteur-récepteur pour leurs échanges optimaux des puissances. Pour être réglée, celle qui voit deux impédances, une côté émetteur-récepteur et une autre côté antenne, doit satisfaire à la règle du « transfert maximal de puissance », (voir la note 1), c’est à dire présenter à l’émetteur-récepteur le conjugué de son impédance, et faire de même, côté antenne, et ce à chaque fréquence de trafic (il sera entendu ici par antenne, aérien et ligne de transmission).

La boîte d’accord est donc un transformateur d’impédances qui ne dissipe pas d’énergie par effet Joule car elle est composée de réactances : une impédance est transformée en une autre en utilisant uniquement des réactances.

Comment les réactances modifient-elles les impédances ? Pour reproduire ce que fait la boîte d’accord, quelles impédances doit-on transformer et en quoi ? Regardons cela à l’aide d’un schéma et voyons ensuite d’un peu plus près la boîte d’accord passe-bas LC-CL et la valeur de ses composants.

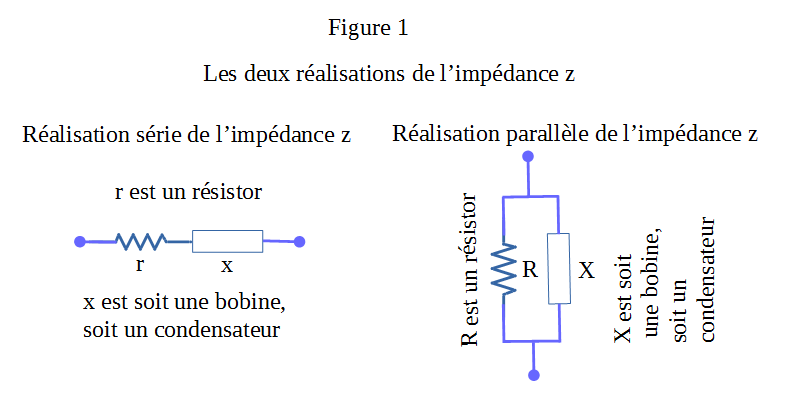
L’impédance, lien entre tension et courant, connue par sa résistance et sa réactance (soit un solénoïde ou bobine, soit un condensateur), peut être réalisée physiquement soit en série, où résistance et réactance sont en série, soit en parallèle où résistance et réactance sont en parallèle (figure 1).

Nous noterons les résistances par les lettres r et R et les réactances par les lettres x et X, en minuscule pour la représentation série, et majuscule pour la représentation parallèle.

Nous écrirons l’impédance z, sous la forme z=(r S x) pour la représentation série, ou z=(R//X) pour la représentation parallèle. Les formules qui permettent de passer d’une représentation à l’autre sont en annexe à la note 2.

La réactance dépend de la fréquence, elle est un nombre positif si inductive, négatif si capacitive, et se calcule à l’aides des formules précisées en annexe à la note 3.

Deux impédances sont dites conjuguées lorsqu’elles ont la même résistance et des réactances dont les effets sont opposés, l’inductif et le capacitif s’annulant mutuellement. Le conjugué de l’impédance z est noté z surligné, z.

Nous ne traiterons ici que d’impédances non purement réactives (r,R ne seront jamais nuls).

Le schéma consiste en deux axes perpendiculaires, l’un horizontal Or et, l’autre vertical x’Ox (figure 2). Sur l’axe horizontal nous placerons les parties résistives des impédances, en Ω, et, sur l’axe vertical nous placerons les parties réactives des impédances, en Ω.

Si la réactance est positive, (impédance inductive), elle sera placée dans le sens Ox, et si elle est négative, (impédance capacitive), elle sera placée dans le sens Ox’.

Notre impédance z=(rSx)=(R//X) sera représentée par un point M du demi-plan (Or, x’Ox). De M abaissons la perpendiculaire à Or qui coupe cet axe en H. OH représente la résistance série de z : OH=r ; la valeur algébrique du segment HM, HM, représente la réactance série de z : x= HM. Menons la perpendiculaire à OM qui coupe les axes Or et x’Ox respectivement en A et B.

Le segment OA représente la résistance parallèle de z : R=OA ; la valeur algébrique du segment OB, OB, représente la réactance parallèle de z : X=OB.

OH=r, OA=R, HM=x, OB=X

Traçons la droite (D) passant par M perpendiculaire à Or et donc parallèle à x’Ox, et traçons le cercle (C) de diamètre OA=R et passant aussi par M. Lorsque que nous faisons varier la réactance x de la représentation série de z en lui mettant en série une réactance modifiante Δx, l’impédance z devenue z’ = (r S x+Δx) se déplace sur la droite (D) que nous nommerons « droite de z », ou « chemin des mises en série ».

Lorsque nous faisons varier la réactance X de la représentation parallèle de z en lui mettant en parallèle une réactance modifiante ΔX, l’impédance z devenue z’ = (R//X.ΔX/[X+ΔX]) se déplace sur le cercle (C) que nous nommerons «cercle de z », ou « chemin des mises en parallèle».

Modifier une impédance quelconque z avec une réactance, soit par mise en série soit par mise en parallèle, c’est se déplacer respectivement soit sur (D), soit sur (C), et nous appellerons cette droite et ce cercle les « chemins de l’impédance z modifiée par réactance  » ou plus simplement « chemins de l’impédance z » puisque nous ne nous intéresserons qu’aux impédances modifiées par des réactances, comme le fait la boîte d’accord (figure 2).

La figure 3 précise le chemin suivi selon la nature de la modification, (série ou parallèle), et selon la réactance utilisée, (bobine ou condensateur). À titre de curiosité les figures 4 et, 5 montrent à l’aide du schéma les déplacements de l’impédance de l’antenne sur les chemins imposés, par une boîte en T, et par une boîte en PI, lorsqu’on se dirige vers l’émetteur-récepteur : imaginez un personnage dans la boîte d’accord regardant l’impédance de l’antenne, puis regardant en se déplaçant plus en arrière ce qu’est devenue cette impédance après que celle-ci ait été modifiée par une réactance série ou parallèle, et ainsi de suite en insérant à nouveau une autre réactance et en regardant en se reculant la nouvelle impédance obtenue, et ce jusqu’à l’émetteur-récepteur (c’est un regard qualitatif à l’aide de la figure 3).

Figure 3

Circulation sur les chemins de z selon la nature de la modification et la nature de la réactance.

Si l’on met en série à z une bobine croissant de 0 à l’infini, le point représentatif de l’impédance modifiée se déplace sur la droite (D) à partir de M dans le sens x’ vers x ; si c’est un condensateur décroissant de l’infini à 0 qui est mis en série le point représentatif de l’impédance modifiée se déplace sur la droite (D) de M dans le sens négatif x vers x’.

Si l’on met en parallèle à z une bobine décroissant de l’infini à 0, le point représentatif de l’impédance modifiée se déplace sur le cercle (C) de M vers O dans le sens anti horaire ; si c’est un condensateur croissant de 0 à l’infini qui est mis en parallèle, le point représentatif de l’impédance modifiée se déplace sur  le cercle (C) de M vers O dans le sens horaire.

Quand nous circulons sur un chemin de z, nous modifions cette impédance, ce chemin reste inchangé, mais l’autre chemin s’en trouve modifié.

En circulant sur la droite de z, nous modifions le diamètre OA=R de son cercle (figure 6a). Le plus petit diamètre pouvant être atteint est OH=r, lorsque z est purement résistive (z=(rS0)=(R//∞), avec r=R). Au-delà de r, il n’y a pas de limite à ce diamètre qui peut être augmenté à volonté. Pour atteindre un cercle choisi il y a deux positions de la droite de z qui le permettent (M est soit en P, soit en N), donc deux impédances qui le permettent, l’une correspondant au point P, et l’autre au point N.

Quand nous circulons sur le cercle de z, nous déplaçons sa droite parallèlement à elle même. Ce déplacement ne peut se faire que sur toute la largeur du diamètre OA=R de son cercle, donc de 0 à R (figure 6b). Ici aussi pour atteindre une droite de position choisie entre 0 et A, il y a deux positions du cercle de z qui le permettent (M va en P ou en N), donc deux impédances, l’une correspondant au point P, et l’autre au point N. Nous n’envisagerons pas d’impédances purement réactives, donc leurs droites ne pourront jamais être superposées à l’axe des réactances x’Ox.

Modifier z par réactance c’est varier la « géométrie » de ses chemins. C’est cette géométrie « variable » des chemins de z qui, si nous arrivons à les arranger pour qu’ils viennent « croiser » ceux d’une autre impédance z’ voulue, choisie, nous permettra de nous rendre à une intersection, changer de chemin, suivre celui de z’, et ainsi facilement la rejoindre. Nous aurons ainsi rendu z égale à z’. Cette géométrie variable, cette propriété, est utilisée par la boîte d’accord et, d’autres équipements d’électronique. Le tableau 1 chiffre ces déplacements et ces déformations. Voyons maintenant les possibilités qu’offre cette géométrie variable due aux réactances pour changer une impédance z en une autre z’.

Sur le schéma de la figure 7 sont portés l’impédance z, son cercle (C), sa droite (D), le cercle (r) de diamètre OH, (OH=r), et la droite (Δ) parallèle à (D) et passant par A, (OA=R). (r) est le plus petit cercle (C) que l’on pourra atteindre en circulant sur (D) ; quant à (Δ) c’est la position extrême de la droite (D) qui pourra être atteinte quand on circule sur (C), ne traitant ici que d’impédances non purement réactives, l’axe x’Ox n’est pas envisagé. Soit maintenant une impédance quelconque z’ de notre schéma. L’idée est la suivante, en déplaçant la droite (D) de z, ou en modifiant son cercle (C), ne pourrait-on pas, soit intercepter, soit se superposer à, l’autre chemin de z’ ? Et alors arrivé sur un chemin de z’ il est très facile de la rejoindre (tableau 1) et nous aurons rendu z égale à z’.

Les cercles forment un faisceau tangents en O ; leur seule intersection est ce point O représentatif des impédances nulles dont nous ne nous servirons pas. Il n’y a pas d’autre intersection possible hormis O, mais nous pouvons utiliser la superposition de cercles. Quant aux droites elles forment un faisceau de droites parallèles et ne pourront être que superposées entre elles. Nous nous servirons donc que de l’intersection entre un cercle et une droite, et des superpositions de droites et de cercles.

Si nous créons une intersection il faut se déplacer une première fois sur un chemin de z et créer cette intersection. Puis nous nous rendrons à cette intersection pour y trouver un chemin de z’, donc second déplacement. Ensuite sur ce chemin de z’ nous nous déplaçons une troisième fois pour la rejoindre. Il nous faut donc trois déplacements, donc trois réactances.

Si nous créons une superposition il faut se déplacer une première fois sur un chemin de z pour atteindre le chemin de z’ et superposer ce chemin de z que nous venons de modifier à celui de z’. Ensuite sur le chemin de z’ nous nous déplacerons une seconde fois pour la rejoindre. Il nous faut donc deux déplacements, donc deux réactances. C’est cette dernière solution que nous exploiterons car elle demande moins de composants.

Si z’ n’est pas à l’intérieur du cercle (r) de z, (figure 7a), le cercle (C) de z va pouvoir être superposé à celui (C’) de z’. Si ces cercles (C) et (C’) sont déjà superposés, c’est à dire que z’ est sur (C), un simple déplacement sur (C) permet de se rendre à z’ (tableau 1). Il y a une solution parallèle pour cela. Si z’ n’est pas sur (C), par déplacement de z sur sa droite (D), on peut superposer son cercle (C) au cercle (C’) de z’. Nous savons que pour ce faire, il y a deux points, P et N de (D) qui le permettent, ces deux points étant confondus en H si le cercle à atteindre (C’) est (r). Il y a deux possibilités série-parallèle chacune nécessitant deux réactances, une possibilité série-parallèle si (C’) est (r).

Si z’ n’est pas au-delà de la droite (Δ), (figure 7b), par déplacement de z sur son cercle (C) on amènera sa droite (D) sur celle (D’) de z’. Si (D) et (D’) sont déjà superposées, c’est à dire que z’ est sur (D), un déplacement de z sur cette dernière le mènera à z’ (tableau 1). Il y a une solution série. Si z’ n’est pas sur (D), par déplacement de z sur son cercle (C), on superposera (D) et (D’). Pour ce faire, il y a deux points P et N de (C) qui le permettent, ces deux points étant confondus en A si z’ est sur (Δ), si (D’) est (Δ), droite où l’on doit superposer (D). Deux possibilités parallèle-série sont applicables, une possibilité parallèle-série si z’ est sur (Δ), et ce nécessitant deux réactances par possibilité.

Si z’ est située à la fois, hors (r) et en deçà de (Δ), il y a donc quatre possibilités pour que z la rejoigne, deux série-parallèle et deux parallèle-série. Si z’ est sur (r) ou sur (Δ) il y a respectivement une solution série-parallèle et une parallèle-série. Si z’ est sur l’un des chemins de z, un simple déplacement sur ce chemin nous suffit, donc une solution.

Nous voyons qu’à une fréquence donnée toute impédance z peut être changée en une autre impédance z’ en utilisant que des réactances. Il y a au moins une possibilité de changement, et au plus quatre. Au minimum une, et au maximum deux réactances suffisent pour chaque changement, en chemin le plus direct. Si deux réactances sont nécessaires, il y en aura une en série, et il y en aura une autre en parallèle car il y a nécessairement un changement de chemin.

Lorsque nous souhaitons changer une impédance z en une autre z’ à une fréquence donnée, nous pouvons déjà voir qualitativement les solutions envisageables ; pour cela portons ces impédances sur le schéma fait grossièrement à main levée en respectant les ordres de grandeur donnés par leurs expressions chiffrées de leurs formes série et parallèle ; les chemins dessinés montrent immédiatement ces solutions. Quantitativement le tableau 2 indique les valeurs des réactances qui permettent le changement d’une impédance z en une autre impédance donnée z’.

La figure 8 est un exemple pour, à la fréquence de 10,125 MHz, changer une impédance z=(39Ω S 2,2µH) en z’=(27Ω S 470pF) (attention, ce schéma n’est pas à l’échelle).

Une bonne aide est un classeur de feuilles calculatrices qui par exemple :

• connaissant le coefficient d’inductance L, la capacité C et, la fréquence f, calcule la réactance

• connaissant la réactance et la fréquence, calcule L et C

• connaissant r et x de z de sa forme série, z=(r S x), calcule R et X de sa forme parallèle z=(R//X) ; et vice-versa

• z et z’ étant données, précise les solutions chiffrées qui changent z en z’ (tableau 2)

Plus tard ce classeur sera à compléter avec la feuille de la boîte d’accord LC-CL.

Quelles impédances la boîte d’accord doit-elle modifier, et en quelle valeurs. Une fois la liaison optimale réalisée, la boîte d’accord ne dissipant pas de puissance, il est certain qu’elle présente le conjugué de l’impédance de l’antenne d’un côté, et le conjugué de celui de l’émetteur-récepteur de l’autre, en vertu du théorème de transfert maximal de la puissance. Pour aboutir à cela, il est suffisant que la boîte d’accord change l’impédance de l’équipement relié d’un côté en conjugué de celle de l’équipement relié sur l‘autre côté, et ainsi ce premier côté présentera l’impédance conjuguée de celle de l’équipement qui lui est raccordé.

En effet, si nous connectons à une transformation le conjugué de ce qu’elle a donné, alors l’impédance qui a servi à faire cette transformation « voit » son conjugué, est connectée à son conjugué (figure 9a) : z changée connectée à son conjugué fait que z voit son conjugué (une transformation est soit une mise en série, soit une mise en parallèle d’une réactance). C’est l’effet miroir du conjugué, qui est obtenu en connectant à une transformation son conjugué.

Si cette impédance z est le résultat d’une autre transformation, ce qui est connecté à cette autre transformation, ce n’est pas z, mais son conjugué puisque z «voit » son conjugué. Par conséquent l’impédance qui a servi à cette autre transformation est connectée sur le conjugué de ce qu’elle a produit, z, et voit son conjugué, est connectée à son propre conjugué ; et ainsi de suite en remontant à la première impédance qui a servi à être transformée (figure 9b). Il y a une propagation en chaîne de l’effet miroir du conjugué tant dans le sens z vers zn que dans le sens inverse zn vers z. Pour obtenir cet effet, il suffit de transformer z en zn et de connecter zn à son conjugué, ou de transformer le conjugué de zn en conjugué de z et de lui connecter z. C’est ce qui se passe dans la boîte d’accord quand elle est réglée, que l’on parte de l’antenne ou de l’émetteur-récepteur.

Si nous souhaitons construire une boîte d’accord nous avons à notre disposition deux transformations au choix pour le calcul de ses réactances constitutives : changer l’impédance de l’antenne en conjugué de celle de l’émetteur-récepteur, ou changer l’impédance de l’émetteur-récepteur en conjugué de celle de l’antenne. Dans cet article le choix qui est adopté est celui de changer l’impédance de l’antenne en conjugué de celle de l’émetteur-récepteur. Nous avons vu comment changer une impédance z en une autre z’, par conséquent si nous mesurons à l’impédance-mètre l’impédance de l’antenne, si nous considérons les transformations qui la changent en conjugué de l’impédance de l’émetteur-récepteur, (qui peut ne pas être purement résistive et donc être quelconque), nous saurons comment confectionner une boîte d’accord «  minimale » avec le minimum de réactances ; d’autres considérations viendront compléter sa constitution (passe-bas, passe-haut, avec transformateur d’isolement, pour lignes équilibrées etc...).

Essayons maintenant d’élaborer une boîte d’accord à la lumière de ce que nous avons vu. Tout au plus deux réactances sont nécessaires pour changer une impédance z en une autre donnée z’ et ces réactances sont câblées soit en parallèle-série, soit en série-parallèle. Nous pouvons envisager une structure en L où une réactance est en série et l’autre en parallèle mais pouvant être positionnée soit à l’entrée, soit à la sortie de celle série, afin d’obtenir une structure soit parallèle-série, soit série-parallèle (figure 10a). Précisons encore notre idée de boîte : qu’elle soit un filtre passe-bas afin d’atténuer les harmoniques source de brouillage . Pour cela l’impédance série sera une bobine, et celle parallèle sera un condensateur. Une armature du condensateur peut être connectée à l’entrée ou à la sortie de la bobine (figure 10b) grâce à un commutateur-inverseur. Nommons boîte LC, (figure 10c), celle où l’antenne est en série avec la bobine, et CL celle où l’antenne est en parallèle avec le condensateur (figure10d). Cet inverseur LC-CL permet en réalité de choisir entre deux boîtes d’accord, deux transformateurs, l’un LC et l’autre CL, étendant ainsi le domaine des impédances qui pourront être transformées par chaque boîte ainsi créée. Posons nous la question de savoir si ces deux boîtes d’accord sélectionnables sont suffisantes pour changer toute impédance en une autre voulue. Recherchons le domaine LC et le domaine CL. Leur réunion fournira celui de la boîte d’accord passe bas LC-CL, et de précieux renseignements sur la plage de couplage de l’antenne à l’émetteur-récepteur. Le câblage série et le câblage parallèle de ces transformateurs LC et CL imposent les chemins aux impédances qui seront transformées. La bobine variable en série, autour de sa valeur initiale, déplace l’impédance z sur sa droite (D). Le condensateur variable en parallèle, autour de sa valeur initiale, déplace l’impédance z sur son cercle (C). La boîte d’accord LC pourrait être appelée boîte d’accord « série-parallèle », et la boîte d’accord CL boîte d’accord « parallèle-série » (ceci en imaginant être dans la boîte un œil côté antenne tout en reculant vers l’émetteur-récepteur ).

La boîte LC va transformer l’impédance z de l’antenne d’abord avec la bobine, puis avec le condensateur et aboutir à l’impédance z’, conjuguée de celle de l’émetteur-récepteur. Le premier chemin imposé par la bobine croissant de 0 à sa valeur maximale, un segment de la droite (D) parcouru dans le sens positif, partant du point représentatif de l’impédance z, va intercepter le dernier chemin à parcourir grâce au condensateur, un arc du cercle (C’) de z’ ; la valeur du condensateur variant de 0 à sa valeur maximale, le chemin à parcourir sur (C’), le sera dans le sens horaire à partir du point représentatif intermédiaire de là où se trouve l’impédance z qui vient d’être modifiée par la bobine. Pour une impédance quelconque de l’émetteur-récepteur, selon que son impédance conjuguée z’ est inductive, capacitive ou résistive pure, la figure 11 précise le domaine de la boîte LC. On remarquera que si l’impédance z’ conjuguée de celle de l’émetteur-récepteur est capacitive, et si celle z de l’antenne est capacitive et a sa résistance série r se situant entre celles série r’ et parallèle R’ de z’ tout en étant extérieure ou sur le cercle(C’), il y a deux chemins qui mènent à z’.

La boîte CL va transformer l’impédance z de l’antenne d’abord avec le condensateur puis avec la bobine et, aboutir à l’impédance z’, conjuguée de celle de l’émetteur-récepteur. Le premier chemin imposé par le condensateur variant de 0 à sa valeur maximale, un arc du cercle (C) de z parcouru dans le sens horaire, va intercepter à partir du point intermédiaire représentatif de là où se trouve l’impédance z qui vient d’être modifiée par le condensateur, le dernier chemin à parcourir grâce à la bobine, croissant de 0 à sa valeur maximale, un segment de la droite (D’) de z’, chemin qui sera parcouru dans le sens positif. Pour une impédance quelconque de l’émetteur-récepteur, selon que son impédance conjuguée z’ est inductive, capacitive ou résistive pure, la figure 12 précise le domaine de la boîte CL. À noter que pour z’ inductive, si z est aussi inductive et est située entre les deux cercles de diamètre r’ et R’, et a une résistance r inférieure à r’, il y a deux chemins qui mènent à z’.

Les figures 11 et 12 montrent que quelle que soit l’impédance d’antenne z, il sera toujours possible de la transformer avec deux réactances tout au plus, afin qu’elle devienne égale à z’ conjuguée de celle de l’émetteur-récepteur. La boîte d’accord passe-bas LC-CL suffit à adapter toute antenne à tout émetteur-récepteur.

Regardons plus précisément les figures où z’ est purement résistive (figures 11c et 12c). C’est le cas de la majorité de nos émetteurs-récepteurs, où r’=R’={impédance d’émetteur-récepteur} et où z’ et son conjugué z’ sont alors identiques : z’=(r’ S 0)=(R’ // ∞)=z’. Le filtre LC, (figure 11c), sera pour les impédances z=(r S x) intérieures ou sur le cercle (C’) de z’ ou bien capacitives, et dont le résistor est inférieur ou égal à R’. Le filtre CL (figure 12c), conviendra aux impédances z=(r S x) dont le résistor est supérieur ou égal à R’ ou aux impédances inductives extérieures ou sur le cercle (C’) de z’. Lorsque l’impédance z est soit sur le demi cercle inductif, soit sur la demie droite capacitive de z’,respectivement une mise en parallèle ou une mise en série permettra de joindre z’.

Le tableau 3 résume toutes ces solutions pour la boîte d’accord LC-CL passe bas où l’émetteur-récepteur a une impédance purement résistive. La figure 13 montre ces domaines. On peut maintenant envisager de compléter le classeur de feuilles de calcul avec la feuille de la boîte LC-CL. Un exemple est donné figure 14 : au feeder de l’antenne à la fréquence de trafic l’impédance est 75Ω, celle de l’émetteur-récepteur est 50Ω ; quelle boîte d’accord passe-bas convient pour adapter ces impédances ?

Voici un regard sur la boîte d’accord lien entre antenne et émetteur-récepteur ; regard sur sa fonction, regard sur l’allure de la modification de ses réactances. Maintes choses peuvent encore y être regardées. Les tensions développées sur ses composants. Sa réponse en fréquence. Le domaine des impédances qui peuvent être changées, domaine fonction des variabilités de ses éléments et de la fréquence, domaine à tracer sur le demi-plan (Or,x’Ox) permettant de dire « ma boîte d’accord permet de connecter à mon émetteur-récepteur les impédances de telle valeur à telle valeur ». Les boîtes d’accord automatiques, comment recherchent-elles l’accord ? Par tâtonnements ? Comment s’y calent-elles ? Une boîte de couplage conçue autour d’une platine à micro-contrôleur, comment mesurer l’impédance, comment calculer et déduire le circuit réactif nécessaire, comment le câbler, comment faire la mise au point fine de l’accord, etc... etc.

Une version au format PDF est disponible en téléchargement dans la rubrique du même nom.